11320. Удивительный трюк

Алиса – фокусница, и она придумала новый трюк. У неё есть n карточек с различными числами от 1 до n, написанными на них. Сначала она просит одного из зрителей перетасовать колоду и выложить карты в ряд. Допустим, что на i-й карте слева стоит число a_i.

Затем Алиса выбирает две перестановки p и q. На p и q есть ограничение – у перестановок не должно быть фиксированных точек. То есть ∀i: p_i ≠ i и q_i ≠ i.

После выбора перестановок Алиса перемешивает карты в соответствии с ними. Теперь i-ой картой слева является карта a[p[q[i]]]. Трюк считается успешным, если на i-ой карте слева после тасования стоит число i.

Помогите Алисе выбрать перестановки p и q или скажите, что это невозможно для заданной перестановки a.

Вход. Первая строка содержит количество тестов t (1 ≤ t ≤ 10⁵).

Каждый тест задается двумя строками. Первая строка содержит одно целое число n (1 ≤ n ≤ 10⁵) – количество карточек. Вторая строка содержит n целых чисел a_i (1 ≤ a_i ≤ n, ∀i ≠ j: a_i ≠ a_j) – начальную перестановку карточек.

Гарантируется, что сумма n по всем тестам не превышает 10⁵.

Выход. Выведите ответ для каждого теста в том же порядке, в котором они появляются во входных данных.

Для каждого теста в отдельной строке выведите “Impossible”, если решение не существует.

В противном случае, в первой строке выведите “Possible”, а в следующих двух строках выведите перестановки p и q.

Пример входа	Пример выхода
4 2 2 1 3 1 2 3 4 2 1 4 3 5 5 1 4 2 3	Impossible Possible 3 1 2 2 3 1 Possible 3 4 2 1 3 4 2 1 Possible 4 1 2 5 3 3 1 4 5 2

РЕШЕНИЕ

комбинаторика

Анализ алгоритма

Рассмотрим три перестановки: a, p, q. Пусть I – тождественная перестановка. Рассмотрим равенство: a(p(q( I ))) = I. Отсюда p(q( I )) = a^-1. Используя тот факт, что перестановка применяется справа налево, указанное тождество можно переписать в виде: p _° q = a^-1. Отсюда следует что q = p^-1 _° a^-1.

Генерируем случайную перестановку p, у которой нет фиксированных точек. После чего вычисляем перестановку q = p^-1 _° a^-1 и тоже проверяем, чтобы у нее не было фиксированных точек. Найденные перестановки p и q являются искомыми.

Пример

Рассмотрим перестановку a = (5, 1, 4, 2, 3).

Обратной к ней будет a^-1 = (2, 4, 5, 3, 1).

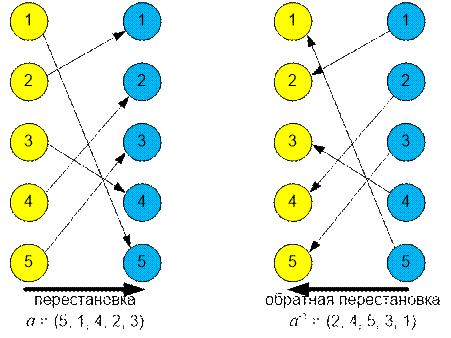
Генерируем случайную перестановку p без фиксированных точек. Пусть, например, p = (4, 1, 2, 5, 3). Вычислим перестановку, ей обратную: p^-1 = (2, 3, 5, 1, 4).

Далее вычисляем q = p^-1 _° a^-1 = (2, 3, 5, 1, 4) _° (2, 4, 5, 3, 1) = (3, 1, 4, 5, 2). Перестановка q не содержит фиксированных точек, поэтому она нам подходит.

Реализация алгоритма

Функция print выводит элементы массива a, начиная с первого.

void print(vector<int>& a)

{

for (int i = 1; i < a.size(); i++)

printf("%d ", a[i]);

printf("\n");

}

Функция is_valid проверяет, содержит ли перестановка v фиксированные точки.

bool is_valid(vector<int>& v)

{

for (int i = 1; i < v.size(); i++)

if (v[i] == i) return false;

return true;

}

Объявим рабочие массивы.

vector<int> a, p, p1, q;

Основная часть программы. Читаем входные данные.

scanf("%d", &tests);

while (tests--)

{

scanf("%d", &n);

Инициализируем массивы.

a.resize(n + 1);

p1.resize(n + 1);

p.resize(n + 1);

q.resize(n + 1);

Читаем входную перестановку a и сразу в массив а заносим перестановку, ей обратную. То есть массив a содержит перестановку a^-1, где a – входная перестановка.

for (i = 1; i <= n; i++)

{

scanf("%d", &x);

a[x] = i;

}

mt19937 – это один из стандартных генераторов псевдослучайных чисел в C++ (Mersenne Twister с периодом 19937). Он очень быстро работает и обладает хорошими статистическими свойствами, что делает его отличным выбором для большинства задач, требующих генерации случайных чисел.

mt19937 gen(random_device{}());

В переменной found будем отмечать, найден ли ответ для текущего теста.

found = false;

Проводим 1000 итераций.

for (it = 0; it < 1000; it++)

{

Генерируем случайную перестановку. Для этого заносим в массив p числа 0, 1, 2, … и при помощи функции shuffle проводим перемешивание элементов, начиная с первого (не нулевого) элемента. Мы работаем с перестановками от 1 до n.

iota(p.begin(), p.end(), 0);

shuffle(p.begin() + 1, p.end(), gen);

Проверяем, является ли перестановка p допустимой (не содержит фиксированных точек).

if (!is_valid(p)) continue;

Вычисляем перестановку p1 = p^-1.

for (i = 1; i <= n; i++)

p1[p[i]] = i;

Вычисляем перестановку q = p1 _° a^-1 = p^-1 _° a^-1.

for (i = 1; i <= n; i++)

q[i] = p1[a[i]];

Если перестановка q является допустимой, то выводим ответ.

if (is_valid(q))

{

puts("Possible");

print(p);

print(q);

found = true;

break;

}

}

Если за 1000 итераций ответ не был найден, то его не существует.

if (!found) puts("Impossible");

}